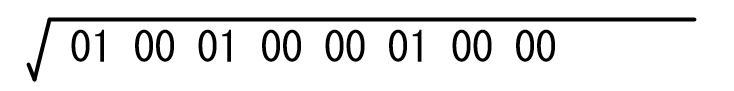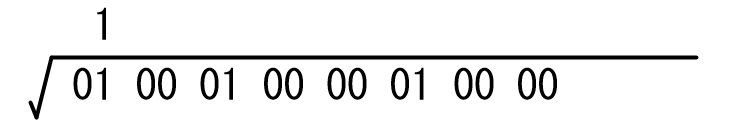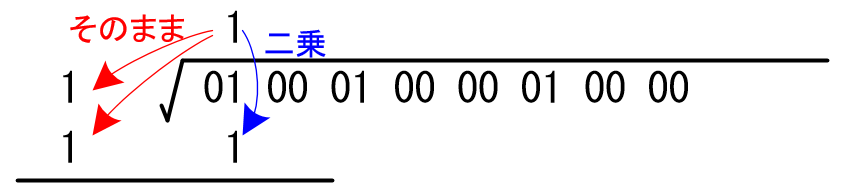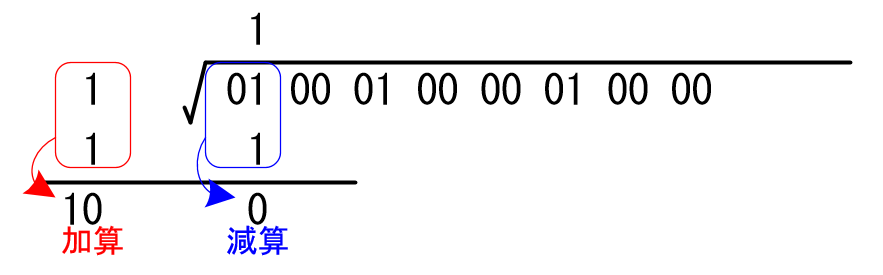Z80で平方根を求めるには?
対象となる数値が数種類しか無い場合は、それらすべての平方根をあらかじめ求めておいて、
どの数値が来たか判定して、その値に対応する「あらかじめ持っている値」を返せば良いです。
それが出来るなら高速です。
しかし、対象となる数値がたくさんある場合(あらかじめ持っている値の容量が許容を超える場合)
計算して求めることになります。
平方根の計算には、「開平法」と呼ばれる方法が一般に知られていますが、乗算・除算と同様に開平法を二進数で
考えることで、1つ1つの演算がシンプルになります。これを利用します。
A = SQRT(HL) を考えるとき、HL が 16bit の符号無し整数で、平方根も整数部だけ得られれば良いとすれば、
HLの平方根は HL半分のbit幅で足りるため、Aレジスタに結果を格納することが出来ます。
開平法を二進数で実施していきます(開平法を知らない方は、他のサイトで調べてきてください)。
17424 の平方根を求める場合を例に挙げます。
17424 を二進数16桁で表記すると 0100010000010000 となります。
これを2桁単位で区切って、区切りとしてスペースを入れておきます。
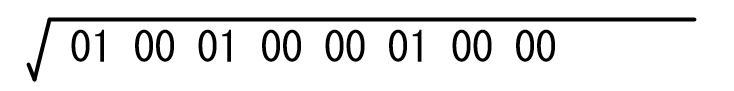
この二桁区切りを左から順に処理していきます。まずは一番左の 01 に着目します。
開平法では、二乗したときにこの数値以下になる一桁の整数を上に立てるのですが、ここは2進数の世界、
1桁は 0 か 1 しかなく、0 を二乗しても 0, 1 を二乗しても 1 という単純な世界です。
つまり 00 の場合は 0, 01, 10, 11 の場合は 1 を立てれば良いことがわかります。
現在着目している二桁は 01 なので、1 を立てますね。
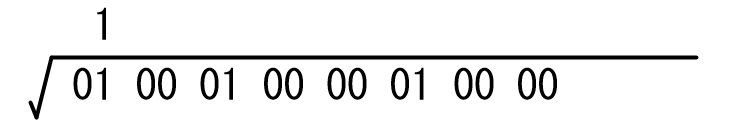
開平法では、その数値を二乗した数値をすぐ下に、そのままの数値を左に2つ書きます。
二乗しても 1 は 1 なので、全部同じモノを書けば良いですね。
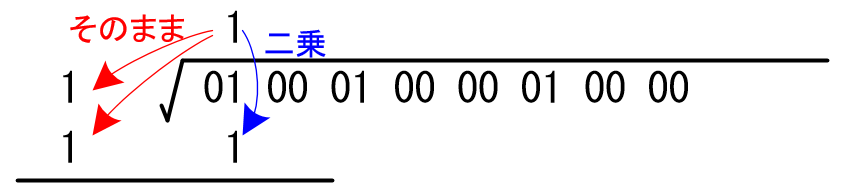
左側に縦に並べた数値は加算して線の下に記入します。
二乗した数値は、そのすぐ上の値から引き算して線の下に記入します。
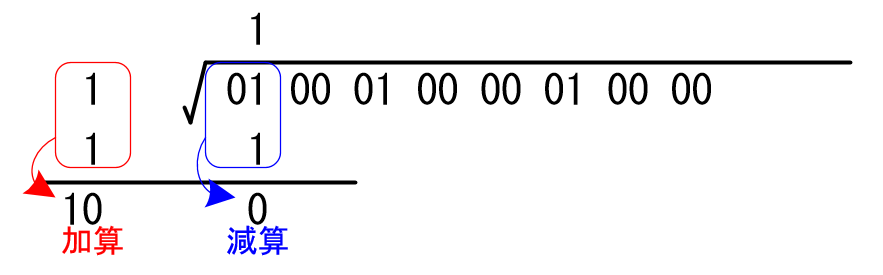
平方根を求めたい値の「次の二桁」をそのまま下ろしてきます。
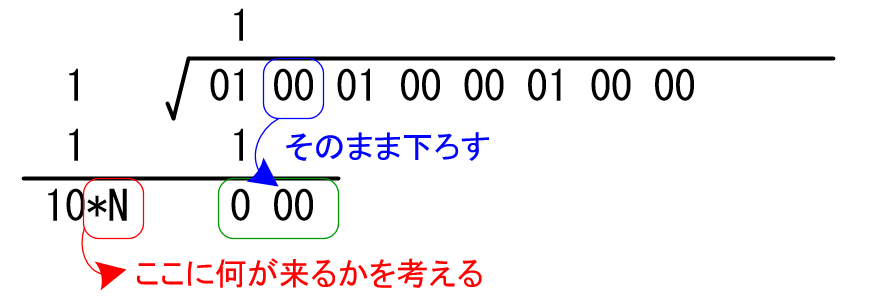
先ほど加算して求めた値に N を掛けるのですが、10*N は、"緑で囲った部分" 以下である最大の N となります。
ここも二進数の世界では簡単になります。
N は 0 か 1 しかあり得ないので、N=1 が緑の値以下なのか、越えてしまうかだけに着目すれば良いです。
今回、緑の値は 000 なので、N=0 になります。
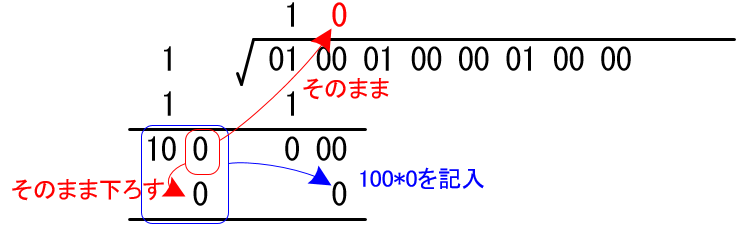
左の領域には、10*N なら 10 0 と記入しておき、その N (今回は 0) の下に、N をもう一つ並べます。
さらに右側の領域には、10*N を計算した値(今回は 10*0 = 0) を下に記入します。
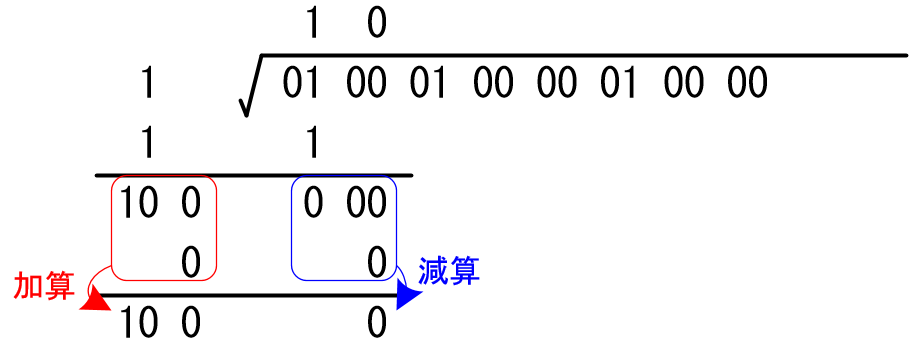
左の領域は2つの値を加算、右の領域は2つの値を減算して線の下に記入します。
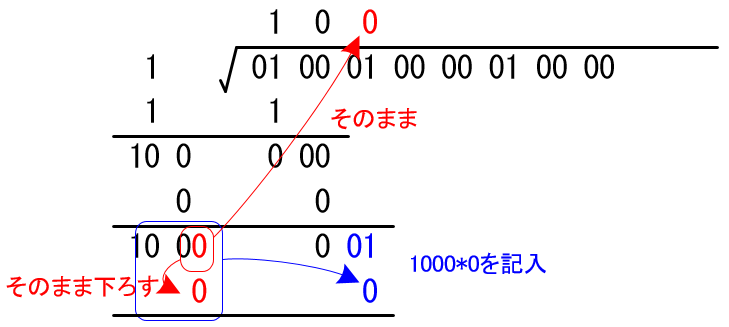
ここからは同じ作業を繰り返していきます。
[次へ][戻る]